XX век - Моррис Клайн. Математика. Утрата определенности



II Расцвет математических истин

Главной целью всех исследований внешнего мира
должно быть открытие рационального порядка и
гармонии, которые бог ниспослал миру и открыл
нам на языке математики,
Иоганн Кеплер
Созданная греками великая цивилизация распалась по нескольким причинам. Первой причиной ее заката было постепенное завоевание римлянами Греции, Египта и Ближнего Востока. Распространяя свое владычество, римляне не ставили целью распространение своей культуры. Завоеванные территории римляне быстро превращали в колонии, из которых грабежом и поборами выкачивали колоссальные богатства.
Другой удар языческой культуре греков нанесло возникновение христианства. Создатели новой религии включили в нее множество греческих и восточных мифов и обычаев с очевидным намерением сделать христианство более доступным для новообращенных, но в то же время заняли непримиримую позицию по отношению к языческой науке и даже осмеивали математику, астрономию и естественные науки. Несмотря на жестокие преследования со стороны римлян, христианство продолжало распространяться и достигло такого могущества, что римский император Константин Великий Миланским эдиктом 313 г. провозгласил христианство официальной религией Римской империи. Несколько позднее Феодосии (правивший в 379 — 392 гг.) запретил языческие религии и в 392 г. приказал разрушить языческие храмы *.
Тысячи греческих книг были сожжены. В 47 г. до н. э. римляне подожгли египетские суда, стоявшие в Александрийской гавани. В огне пожара, охватившего город, погибла знаменитая Александрийская библиотека — ценнейшее собрание древних рукописей. В тот год, когда Феодосий запретил языческие религии, христиане разрушили храм Сераписа в Александрии — хранилище уникального собрания уцелевших греческих рукописей. Многие сочинения греческих авторов, написанные на пергаменте, были стерты христианами, которые использовали этот пергамент для записи собственных текстов религиозного содержания.
Последующая история Римской империи также имеет непосредственное отношение к интересующей нас теме. Император Феодосий разделил необъятную империю между двумя своими сыновьями — Гонорием, которому отошла Италия и Западная Европа, и Аркадием, получившим в наследство Грецию, Египет и Ближний Восток. Западная часть Римской империи была завоевана в V в. готами, и ее дальнейшая история относится уже к истории средневековой Европы. Восточная часть Римской империи сохранила независимость. В состав Восточной Римской империи, известной также под названием Византийской империи, входили собственно Греция и Египет, что в какой-то мере способствовало сохранению греческой культуры и сочинений греческих ученых.
Завоевание Египта (640 г.) сторонниками набиравшего силу ислама нанесло греческой культуре удар, от которого она уже не смогла оправиться. Все ранее уцелевшие книги были уничтожены; как говорит предание, халиф Омар провозгласил: «Либо в этих книгах написано то, что есть в Коране, и тогда нам незачем их читать, либо они утверждают то, что противоречит Корану, и тогда их не подобает читать». Почти полгода бани Александрии отапливались пергаментными свитками.
После захвата Александрии приверженцами пророка Мухаммеда (Магомета) большинство ученых уехали в Константинополь, ставший столицей Восточной Римской империи. И хотя традиционная греческая культура не могла процветать в неблагоприятной для нее атмосфере Византии, приток ученых и возможность продолжать научную работу в условиях относительной безопасности способствовали приумножению сокровищницы знаний, ставшей через 800 лет достоянием Европы.
Свой вклад в дальнейшее развитие математики как науки внесли индийцы и арабы. Некоторые идеи индийских и арабских математиков сыграли немалую роль в дальнейшем *. За тысячелетие (200 — 1200 гг.) индийцы (не без влияния греческих источников) получили важные результаты в области арифметики и алгебры. Арабы — созданный ими Арабский халифат в период расцвета простирался по всему побережью Средиземного моря, глубоко вторгался на Ближний Восток и объединял разноплеменные народы, исповедовавшие ислам,— усвоили лучшие достижения греческой и индийской математики и получили ряд новых результатов. Действуя в духе греков александрийского периода, арабы в своих трудах опирались и на дедуктивные рассуждения, и на эксперимент. Арабские ученые сказали свое слово в алгебре, географии, астрономии и оптике. Заботясь о передаче знаний грядущим поколениям, арабы создавали школы и даже высшие учебные заведения. К чести арабов следует заметить, что, будучи ревностными приверженцами своей религии, они тем не менее считали недопустимым ограничивать религиозными догмами математические и естественнонаучные исследования.
Хотя индийцы и арабы основывали свои исследования на прочном фундаменте, воздвигнутом греками, и внесли свой вклад в дальнейшее развитие эллинской математики и естествознания, они не смогли в такой мере, как греки, проникнуться пониманием структуры Вселенной. Арабы переводили труды греческих ученых и составляли к ним обширные комментарии, в том числе и критические, но их достижения не пополнили сокровищницу знаний, накопленных их предшественниками, сколько-нибудь существенно [см., впрочем, [9], гл. III]. К 1500г. Арабский халифат распался, теснимый христианами на Западе и раздираемый междоусобицами на Востоке.
В то время как арабы строили и расширяли свою цивилизацию, в Западной Европе зарождалась новая цивилизация. В период средневековья (500 — 1500 гг.) в этой части мира был достигнут высокий уровень культуры. В европейской культуре того времени безраздельно господствовала христианская религия, а ее доктрины, при их определенных достоинствах, отнюдь не способствовали познанию физического мира. Вселенной, как утверждали отцы церкви, правит бог, и роль человека сводится к безропотному служению богу и снисканию милости божьей в надежде на спасение, дабы душа в загробном мире обрела радость и вечное блаженство. Земному существованию не следует придавать особого значения; трудности и страдания надлежит переносить с кротким терпением, ибо господь ниспосылает их, чтобы испытать, крепка ли вера человека. Нужно ли говорить, что в подобных условиях интерес к математике и естественным наукам, стимулом которого в античности служило изучение физического мира, переживал глубокий кризис. Мыслители средневековой Европы были ревностными искателями истин, но искали их в прилежном изучении Священного писания, а не в познании природы. Тем не менее в позднем средневековье философия поддерживала убеждение в правильности и постоянстве управляющих природой механизмов, хотя и считала, что в природе все происходит по воле божьей.
В конце периода средневековья Европа испытала поистине революционные потрясения, которые привели к значительным изменениям. Среди многих причин, способствовавших превращению средневековой цивилизации в современную, самой важной с точки зрения интересующей нас темы было пробуждение интереса к трудам греческих авторов и вновь начавшееся изучение их. Сочинения античных ученых становились известными в арабских переводах и через оригиналы, сохранившиеся в Византийской империи. После завоевания Византии турками в 1453 г. многие греческие ученые, захватив с собой книги, бежали на Запад. Именно из сочинений греков ведущие европейские мыслители того времени узнали, что природа построена на математических принципах и что план творения гармоничен, эстетически привлекателен и являет собой сокровенную истину о природе. Природа не только рациональна и упорядочение, но и действует в соответствии с неизбежными и неизменными законами. Европейские ученые приступили к исследованию природы как последователи древнегреческих философов.
Не подлежит сомнению, что многих европейских ученых побудило приступить к изучению природы возрождение греческих идеалов. Но темпы и широкий размах возрождения математики и естествознания были обусловлены и многими другими факторами. Силы, приводящие к крушению одной и вызывающие развитие другой культуры, многообразны и сложны. Процесс зарождения науки изучали многие ученые, и немало трудов по истории посвящено выяснению его причин. Мы ограничимся здесь кратким перечислением факторов, обусловивших тот интеллектуальный переворот, который ныне именуют Возрождением.
Возникновение класса свободных ремесленников небывало повысило интерес к материалам, способам их обработки и технологии, породив новые научные проблемы. Географические исследования, вызванные необходимостью поиска новых источников сырья и золота, способствовали распространению знаний о неведомых ранее странах и обычаях, бросавших своего рода вызов средневековой европейской культуре. В эпоху Реформации были отвергнуты многие католические доктрины, что усилило споры и даже скептицизм в отношении не только католицизма, но и протестантизма. Значение, которое пуритане придавали труду и полезности знаний, внедрение пороха, поставившее перед европейцами новые задачи военного характера (например, изучение траекторий пушечных ядер 2), проблемы, связанные с плаванием в открытом море за тысячи миль от берега,— все это создавало благоприятную атмосферу для исследования природы. Изобретение книгопечатания способствовало распространению знаний, за чем, однако, неусыпно следила церковь. И хотя специалисты расходятся во мнениях относительно того, в какой мере те или другие силы повлияли на изучение природы, для наших целей достаточно отметить одновременное влияние многих факторов и тот общепризнанный факт, что научные знания и стремления к их приобретению стали отличительной чертой современной европейской цивилизации.
В целом европейцы далеко не сразу откликнулись на новые веяния. В эпоху Возрождения для европейцев было более характерно изучение сочинений греческих авторов, чем следование греческим идеалам (см., например, [10]). Но к началу XVI в. провозглашеннные греками цели научного исследования — изучение явлений природы на рациональной основе и поиск лежащего в их основе общего математического плана — проникли в умы европейцев. И тут европейцы столкнулись с серьезной проблемой: поставленные греками цели находились в противоречии с господствовавшей тогда в Европе культурной традицией. В то время как греки верили в математические принципы, лежащие в основе природы, в природу, неизменно и неукоснительно следующую некоторому идеальному плану, мыслители позднего средневековья приписывали и сотворение «плана», и все происходящее в природе христианскому богу. Он был творцом и создателем — и все в природе неукоснительно следовало его плану. Вселенная была творением бога и беспрекословно подчинялась его воле. Математики и представители естественных наук в эпоху Возрождения и на протяжении нескольких последующих столетий были правоверными христианами и полностью принимали эту доктрину. Но греческое учение о математических принципах устройства Вселенной противоречило догматам католической церкви. Каким же образом можно было примирить попытки понять Вселенную, сотворенную богом, с поисками математических законов мироздания? Примирить, казалось бы, непримиримое можно было, только создав новую доктрину, согласно которой христианский бог при сотворении Вселенной руководствовался математическими принципами. Так католическая доктрина, провозглашавшая первостепенной обязанностью постижение божьей воли и его творений, обрела форму поиска математического плана, по которому бог создал Вселенную. И действительно, как мы вскоре убедимся, работы математиков в XVI—XVII вв. и на протяжении большей части XVIII в. носили характер религиозного поиска. Открытие математических законов природы было своего рода откровением, являвшим людям славу и величие божьего творения. Математическое знание (истина о замысле творца) было священным, как любая строка Библии. Разумеется, человек не мог надеяться постичь божественный план с такой же полнотой и ясностью, как сам господь бог, но человек мог по крайней мере со всей кротостью и смирением приблизиться к пониманию замысла творца и, следовательно, к пониманию созданного им мира.
Можно пойти дальше и утверждать, что математики того времени были уверены в существовании математических законов, лежащих в основе явлений природы, и настойчиво искали эти законы, будучи a priori убеждены в осмысленности своих поисков: ведь бог, создавая Вселенную, не мог не запечатлеть в ней математические законы. Каждое открытие закона природы провозглашалось еще одним подтверждением не столько мудрости исследователя, совершившего открытие, сколько божьей милости. Такие взгляды и убеждения математиков и естествоиспытателей являлись отражением всей интеллектуальной атмосферы, типичной для Европы эпохи Возрождения. Незадолго до того вновь открытые сочинения греческих авторов чем-то противоречили христианской культуре, пропитанной глубокой набожностью; однако духовные вожди эпохи Возрождения, взращенные в христианской традиции и одновременно испытавшие на себе притягательную силу греческой культуры, сумели соединить эти два течения, казалось бы противоречащие одно другому.
Наиболее ярким примером происходившего в Европе слияния греческого учения о «математизированной» Вселенной с характерной для эпохи Возрождения верой в божественное ее происхождение являются труды Николая Коперника и Иоганна Кеплера. Вплоть до XVI в. единственной надежной и практически применимой астрономической теорией была геоцентрическая система Гиппарха и Птолемея. Она была принята профессиональными астрономами и использовалась при составлении календарей и в навигационных расчетах. К работе над созданием новой астрономической теории приступил Коперник (1473—1543). Астрономию он изучал в Болонском университете, куда поступил в 1497 г. В 1512 г. Коперник приступил к исполнению обязанностей каноника Фромборкского собора в Вармии. Положение члена капитула оставляло Копернику немалый досуг для астрономических наблюдений и обдумывания будущей теории. После многолетних размышлений и наблюдений Коперник создал новую теорию движения планет, изложив ее в своем классическом труде «Об обращениях небесных сфер» [11]. Первый вариант рукописи Коперник закончил еще в 1507 г., но медлил с публикацией, опасаясь противодействия со стороны церкви. Книга Коперника вышла из печати в 1543 г.— в год его смерти.
В те времена, когда Коперник принялся размышлять на астрономические темы, теория Птолемея претерпела некоторые усовершенствования. К эпициклам, введенным Птолемеем, добавились новые эпициклы, которые понадобились для того, чтобы привести теорию в соответствие с новыми астрономическими данными, собранными главным образом арабами. Во времена Коперника для описания движений Солнца, Луны и пяти известных в тот период планет птолемеевой теории требовалось уже семьдесят семь кругов. Многие астрономы, как о том упоминает Коперник в предисловии к своему сочинению, стали считать теорию Птолемея чрезмерно сложной.
Изучение достижений греческих ученых привело Коперника к убеждению в существовании единого математического плана, по которому построена Вселенная и который обеспечивает ее гармонию. Эстетические соображения требовали наличия более изящной теории, чем то сложное нагромождение эпициклов, которое содержалось в позднем варианте теории Птолемея. Из прочитанных книг Коперник узнал, что некоторые греческие авторы, главным образом Аристарх Самосский (III в. до н. э.) 3, высказывали предположение, что Солнце покоится, а Земля обращается вокруг него и одновременно поворачивается вокруг своей оси, и он решил выяснить, к чему может привести подобная гипотеза.
Поворотный момент в размышлениях Коперника наступил тогда, когда он воспользовался для описания движений небесных тел птолемеевой схемой деферента и эпицикла (гл. I), с тем, однако, существенным различием, что в центре каждого деферента находилось Солнце. Земля также стала одной из планет, которая, вращаясь вокруг своей оси, движется по эпициклу. Такое видоизменение позволило Копернику значительно упростить всю схему. В предложенной им гелиоцентрической системе оказалось возможным уменьшить общее число кругов (деферентов и эпициклов) до тридцати четырех вместо семидесяти семи кругов геоцентрической теории.
Еще более замечательное упрощение ввел Иоганн Кеплер (1571— 1630) — одна из самых удивительных фигур в истории науки. Жизнь Кеплера омрачалась множеством личных несчастий и трудностей, вызванных религиозными и политическими событиями. В 1600 г. ему посчастливилось стать ассистентом знаменитого астронома Тихо Браге, производившего многочисленные астрономические наблюдения и систематизировавшего полученные результаты,— это была первая крупная попытка такого рода со времен античности. Наблюдения Тихо Браге и небольшое число наблюдений, произведенных самим Кеплером, оказались для последнего бесценными. После смерти Браге в 1601 г. Кеплер стал его преемником на посту придворного математика австрийского императора Рудольфа II.
Научные рассуждения Кеплера поражают необузданной фантазией. Подобно Копернику, Кеплер был склонен к мистике и разделял убеждение в том, что мир создан богом в соответствии с простым и исполненным красоты математическим планом. В своем сочинении «Космографическая тайна» (1596) Кеплер утверждал (1121, с. 176), что «сущность трех вещей... а именно: число, размеры и движения небесных орбит» — заключена в гармонии замысла, которым всеблагой и всемогущий бог руководствовался при сотворении мира. Мысль о гармонии мира стала у Кеплера доминантой. Но Кеплер был наделен всеми качествами, которыми, по нашим критериям, должен обладать ученый. Он умел, если было нужно, обуздывать свою неуемную фантазию, подчиняя ее холодному рационализму. Хотя его богатое воображение живо откликалось на любые новые теоретические концепции, обладающие эстетической привлекательностью, Кеплер сознавал, что теория должна находиться в согласии с наблюдениями, а к концу жизни с еще большей отчетливостью понял, что эмпирические данные могут подсказать исследователю фундаментальные принципы науки. Кеплер безжалостно отбрасывал самые привлекательные и многообещающие математические гипотезы, если оказывалось, что они не согласуются с наблюдениями, и именно это невероятное упорство в неприятии даже самых незначительных расхождений между теорией и наблюдениями, с которыми легко смирился бы любой другой ученый того времени, позволило Кеплеру стать творцом новых научных идей, решительно порывающих с многовековой традицией. К тому же Кеплер обладал скромностью, терпением и энергией, т. е. всеми теми качествами, которые позволяют великим людям выполнять возложенную на них нелегкую миссию.
Предпринятый Кеплером поиск математических законов природы, в существовании которых он был глубоко убежден, поначалу складывался неудачно: не один год ушел на проверку неверных гипотез. В предисловии к «Космографической тайне» Кеплер так формулирует программу своего сочинения:
Я вознамерился доказать, что всеблагой и всемогущий бог при сотворении нашего движущегося мира и при расположении небесных орбит избрал за основу пять правильных тел, которые со времен Пифагора и Платона и до наших дней снискали столь громкую славу, выбрал число и пропорции небесных орбит, а также отношения между движениями в соответствии с природой правильных тел [имеются в виду так называемые платоновы тела — правильные тетраэдр, гексаэдр (куб), октаэдр, икосаэдр и додекаэдр.— Ред.] ([12], с. 176.)
Однако попытка раскрыть «тайну мироздания» на этой основе оказалась безуспешной: выводы теории, построенной на свойствах пяти правильных тел, расходились с результатами наблюдений, и, перепробовав множество вариантов в надежде спасти полюбившуюся ему идею, Кеплер был вынужден отказаться от намеченного подхода.
Зато необычайным успехом увенчались более поздние попытки Кеплера найти в природе гармонические математические отношения. Наиболее известные и значительные из полученных им результатов известны ныне под названием три закона Кеплера (законы движения планет). Первые два закона были опубликованы Кеплером в сочинении, вышедшем в 1609 г. под весьма длинным названием, так что обычно при ссылках на эту работу приводят либо начало названия — «Новая астрономия», либо его заключительную часть — «Комментарии о движении планеты Марс». Особенно замечателен первый закон Кеплера, ибо, сформулировав его, Кеплер порвал с двухтысячелетней традицией, согласно которой небесные тела должны обязательно двигаться по кругам или сферам. Кеплер отказался от деферента и нескольких эпициклов, к которым прибегали при описании движения любой планеты и Птолемей, и Коперник, и показал, что для описания движения планеты достаточно указать один-единственный эллипс. Первый закон Кеплера гласит: каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце (рис. 2.1). Другой фокус любой эллиптической орбиты представляет собой «пустую» математическую точку, в которой ничего не находится. Первый закон Кеплера имеет первостепенное значение, поскольку позволяет легко и просто представить орбиты планет. Разумеется, Кеплер, как и Коперник, добавляет, что, описывая свою эллиптическую траекторию, Земля одновременно вращается и вокруг своей оси.
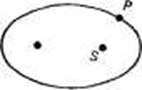
Рис. 2.1. Первый закон Кеплера. Планеты движутся по эллипсам, в одном из фокусов которого находится Солнце
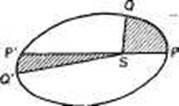
Рис. 2.2. Второй закон Кеплера: если дуги PQ и P'Q' орбиты планета проходит за одно и то же время, то площади секторов PSQ и P SQ равны.
Но чтобы быть полезной, астрономии следует идти гораздо дальше: она должна уметь предсказывать положения планет. Если мы обнаружим, что какая-то планета в момент наблюдения находится, скажем, в точке Ρ (рис. 2.1), то нам может понадобиться узнать, когда она будет находиться в каком-либо другом положении, например в точке солнцестояния или равноденствия. А чтобы ответить на этот вопрос, необходимо знать, с какой скоростью планета движется по своей траектории.
Пытаясь найти скорость планеты, Кеплер сделал еще один решающий шаг. Коперник и греческие мыслители считали скорости планет постоянными. Планета у них двигалась по эпициклу равномерно, проходя равные дуги окружности за равные промежутки времени, а центр каждого эпицикла перемещался с постоянной скоростью по другому эпициклу или по деференту. Из наблюдений Кеплер знал, что планета движется по эллиптической орбите с изменяющейся скоростью, и в результате долгих и трудных поисков нашел правильный закон изменения скоростей. Кеплер открыл, что если планета, двигаясь по орбите, перемещается из точки Ρ в точку Q (рис. 2.2), например, за один месяц, то на перемещение из точки Р' в точку Q' е": также потребуется один месяц при условии, что площадь сектора PSQ равна площади сектора P'SQ'. Так как точка Ρ расположена ближе к Солнцу, чем точка Ρ', то дуга PQ должна быть длиннее дуги P'Q', если площади секторов PSQ и P'SQ' равны. Следовательно, планеты движутся по орбитам с переменной скоростью: чем ближе к Солнцу, тем быстрее.
Открыв второй закон (равенства секториальных скоростей), Кеплер был необычайно рад. Хотя пользоваться вторым законом не так просто, как законом постоянства скоростей, совершенное открытие подкрепило глубочайшую убежденность Кеплера в том, что господь бог, создавая Вселенную, руководствовался математическими принципами. Бог действовал чуть более изощренно, чем предполагали предшественники Кеплера, но теперь со всей очевидностью было установлено, что скорости движения планет по орбитам подчиняются математическому закону.
Но еще одна важная проблема по-прежнему оставалась нерешенной: по какому закону изменяются расстояния, отделяющие планеты от Солнца? Проблема осложнялась тем, что расстояние от планеты до Солнца не постоянно. И Кеплер принялся за поиск нового принципа, учитывающего зависимость расстояния от времени. По его глубокому убеждению бог сотворил мир не только на основе математических принципов, но и гармонично, причем слово «гармония» Кеплер понимал в самом прямом смысле. Так, он верил в существование музыки сфер, образующей гармонические созвучия, которые, хотя и невоспринимаемы на слух, но тем не менее их можно обнаружить при надлежащем «переводе» особенностей движения планет на ноты. Следуя этой путеводной идее и основываясь на поистине удивительной комбинации аргументов музыкального и математического характера, Кеплер устанавливает, что если Т—период обращения планеты вокруг Солнца, a D — среднее расстояние от планеты до Солнца, то Т2=KD3, где k — постоянная, одинаковая для всех планет. Это утверждение и есть третий закон Кеплера для движения планет, торжественно провозглашенный им в сочинении «Гармония мира» (1619).
Сформулировав третий закон, Кеплер разражается ликующим хвалебным гимном богу-творцу: «Вы, Солнце, Луна и планеты, восславьте его на своем неизъяснимом языке! Вы, небесные гармонии и все, кто постигает разумом его чудесные творения, воздайте ему хвалу! И ты, душа моя, восхвали создателя! Им все сотворено, и в нем все существует. Все лучшее из того, что мы знаем, заключено в нем и в нашей жалкой науке».
О том, с какой силой Коперник и Кеплер верили, что бог сотворил мир гармоничным и простым, можно судить по тем возражениям, с которыми им приходилось сталкиваться. Даже по теории Птолемея все остальные планеты, кроме Земли, находились в движении, и это объяснялось особо легкой и потому легко приводимой в движение субстанцией, из которой якобы сотворены планеты Но что могло привести в движение тяжелую Землю? Ни Коперник, ш Кеплер не могли ответить на этот вопрос. Не принимая идею о суточном вращении Земли вокруг собственной оси, противники ее ссылались на такой, казалось бы, очевидный факт: тела не могли бы I удержаться на поверхности вращающейся Земли и, сорвавшись с нее, улетели бы в космическое пространство, подобно тому как срываются предметы с вращающейся платформы. Против столь «неопровержимого» аргумента невозможно было возразить! Весьма неубедительным был ответ Коперника и на другой довод против суточного вращения Земли: вращающаяся Земля должна просто-напросто разлететься на части. На это Коперник возражал, что вращение Земли естественно и потому не может разрушить нашу планету. Должно быть, ощущая шаткость этого аргумента, Коперник, переходя в «контрнаступление», спрашивал, почему в таком случае небо не разлетается на части в результате очень быстрого суточного вращения, предусматриваемого геоцентрической теорией. Еще один довод против суточного вращения Земли состоял в следующем: если бы Земля вращалась с запада на восток, то любой предмет, подброшенный в воздух, отклонялся бы к западу, так как Земля под ним успевала бы поворачиваться. А если бы Земля к тому же обращалась вокруг Солнца, то более легкие предметы на Земле отставали бы от более тяжелых, поскольку скорости падающих предметов, как утверждали греки и продолжали считать ученые эпохи Возрождения, пропорциональны их весу. На это Коперник возражал, что воздух обладает земной природой и поэтому движется в полном соответствии с движением Земли. Суть всех этих возражений против суточного вращения Земли и ее обращения вокруг Солнца сводилась к тому, что движение Земли не вписывалось в рамки общепринятой во времена Коперника и Кеплера теории движения, предложенной еще Аристотелем.
Ряд научных возражений против гелиоцентрической теории выдвигала и сама астрономия. Наиболее серьезное возражение вызывало то, что в гелиоцентрической теории звезды считались неподвижными. Но за полгода Земля перемещалась в пространстве на расстояние около 300 млн. км. Следовательно, если наблюдатель заметит направление на какую-нибудь звезду, то спустя полгода он должен обнаружить, что это направление изменилось. Во времена же Коперника и Кеплера такого рода изменения в направлениях на звезды обнаружены не были. На это возражение Коперник отвечал, что звезды расположены слишком далеко от Земли и поэтому направления на звезды изменяются незначительно. Его ответ не удовлетворил критиков, заметивших, что если бы звезды были так далеки, как утверждает Коперник, то их нельзя было бы наблюдать. Тем не менее ответ Коперника был правильным. Направление на ближайшую звезду изменяется за полгода всего лишь на 0,31", и впервые это было обнаружено в 1838 г. немецким астрономом Фридрихом Вильгельмом Бесселем, имевшим в своем распоряжении хороший телескоп.
Сторонники геоцентрической теории спрашивали также, почему мы не ощущаем движения Земли, если та обращается вокруг Солнца со скоростью около 30 км/с, а скорость вращения вокруг собственной оси достигает на экваторе величины около 0,8 км/с? К тому же наши глаза убеждают нас в том, что Солнце обращается вокруг Земли. Для современников Кеплера ссылка на то, что мы не ощущаем движения с огромными скоростями, в котором сами участвуем, если верить новой астрономии, была неоспоримым контрдоводом. Все научные возражения против движения Земли были достаточно весомыми — от них нельзя было отмахнуться, как от брюзжания упрямцев, не желающих признать очевидную истину.
Коперник и Кеплер были людьми глубоко религиозными, и все же они оба дерзнули отказаться от одной из основных догм христианства: человек есть центр Вселенной и средоточие всех помыслов божьих. Гелиоцентрическая теория, поместив в центре Вселенной Солнце, подорвала столь успокоительную догму церкви. Человек стал одним из множества «странников», влекомых Землей в холодных небесных прссторах. Утверждение церковников о том, будто человек рожден для того, чтобы прожить славную жизнь и обрести райское блаженство после смерти, стало казаться весьма сомнительным. Утратило правдоподобие и утверждение о том, будто человек является объектом особого Е:;КМЗНИЯ со стороны господа бога. Коперник подорвал тезис о том, будто бы Земля является центром Вселенной, указав, что размеры Вселенной огромны и поэтому бессмысленно говорить о каком бы то ни было центре Вселенной. Но в глазах его современников это рассуждение вовсе не выглядело убедительным.
И все же у Коперника и Кеплера был аргумент, перевешивавший все возражения против гелиоцентрической системы мира: им удалось построить более простую в математическом отношении, более гармоничную и эстетически более привлекательную теорию. Но если новая теория превосходит в математическом отношении старую, то для всякого, кто считал, что бог сотворил мир, используя при этом лучшую из теорий, любые сомнения в правильности гелиоцентрической теории должны были отпасть.
И в сочинении Коперника «О обращениях небесных сфер», и в многочисленных трудах Кеплера имеется немало высказываний, убедительно свидетельствующих, что Коперник и Кеплер были уверены в правильности построенной ими теории. Например, у Кеплера мы находим следующий отзыв о построенной им теории движения планет по эллиптическим орбитам: «Я клятвенно подтверждаю ее правильность и созерцаю ее красоту с неизъяснимым, переполняющим душу восторгом». Само название кеплеровского сочинения 1619 г.— «Гармония мира» и бесконечные дифирамбы богу, исполненные восхищения перед величием божественного математического плана, отражают убежденность Кеплера в правильности найденного им закона.
Сначала новая теория получила поддержку лишь у математиков. И это не было неожиданным. Только математики были убеждены в том, что Вселенная построена на простых математических принципах, только у математиков хватило интеллектуальной смелости, чтобы преступить через широко распространенные философские, религиозные и научные контраргументы и по достоинству оценить математические преимущества новой, революционной астрономии. Нужно было обладать неколебимой уверенностью в значимости математических принципов, на которых зиждется Вселенная, чтобы отстаивать новую теорию перед лицом сильнейшей оппозиции.
Однако затем гелиоцентрическая теория получила неожиданное подкрепление. В начале XVII в. был изобретен телескоп, и Галилей, прослышав об этом изобретении, сам построил телескоп и приступил к наблюдениям неба. Результаты наблюдений повергли в изумление современников Галилея. Он обнаружил у Юпитера четыре луны (в современные телескопы мы можем наблюдать 12 спутников Юпитера). Это открытие означало, что у движущейся планеты могут быть естественные спутники. Галилей наблюдал неровности и горы на поверхности Луны, пятна на Солнце, странные выступы по обе стороны экватора на Сатурне (сейчас мы знаем, что за выступы Галилей принял кольца Сатурна). Эти наблюдения явились еще одним свидетельством того, что планеты схожи с Землей и заведомо не являются идеальными телами, состоящими, как полагали греки и средневековые мыслители, из какого-то особого эфирного вещества. Млечный Путь, ранее казавшийся широкой светлой полосой, при наблюдении в телескоп «распался» на мириады звезд. В небесах были рассеяны множества других солнц и, возможно, другие планетные системы. Коперник предсказывал, что если бы человеческое зрение было более острым, то человек мог бы наблюдать фазы Венеры и Меркурия так же, как он может невооруженным глазом наблюдать различные фазы Луны. С помощью телескопа Галилей обнаружил фазы Венеры. Произведенные наблюдения убедили Галилея в правильности теории Коперника, и в своем классическом труде «Диалог о двух главнейших системах мира — птолемеевой и коперниковой» (1632) он решительно выступает в защиту новой теории. Теория Коперника завоевала признание еще и потому, что позволяла астрономам, географам и мореплавателям упростить вычисления. К середине XVII в. научный мир принял гелиоцентрическую систему. Уверенность в истинности математических законов природы возросла неизмеримо.
Отстаивать тезисы об обращении Земли вокруг Солнца и о суточном вращении Земли вокруг своей оси в интеллектуальной атмосфере начала XVII в. было отнюдь не просто. Всем известно о процессе, который инквизиция устроила над Галилеем. Набожный католик Паскаль обнаружил свои сочинения в Индексе запрещенных книг за то, что в «Письмах к провинциалу» опрометчиво выразил порицание иезуитам:
Напрасно также было с вашей стороны испрашивать в Риме декрет об осуждении мнения Галилея относительно движения Земли. Не этим будет доказано, что она стоит неподвижно; если бы имелись несомненные наблюдения, которые доказали бы, что именно она-то и вращается, το все люди в мире не помешали бы ей — вращаться, и себе — вращаться вместе с нею. ([13], с. 336.)
Коперник и Кеплер, не усомнившись, приняли синтез греческого учения о природе, основанной на математических принципах, и католического догмата о боге — творце и создателе Вселенной. Рене Декарт (1596—1650) вознамерился развить новую философию науки систематически, ясно и обоснованно. Декарт прежде всего был философом, во-вторых, он занимался проблемами космологии, в-третьих, был физиком, в-четвертых,— биологом и, только в-пятых,— математиком, хотя он и считается одним из основных творцов новой математики. Философия Декарта имеет весьма важное значение, поскольку именно она оказала решающее влияние на формирование самого стиля мышления, характерного для XVII в., и на таких гигантов, как Ньютон и Лейбниц4. Свою главную цель Декарт видел в нахождении способа, позволяющего устанавливать истину в любой области, и посвятил ей основной труд — «Рассуждение о методе, чтобы хорошо направлять свой разум и отыскивать истину в науках» (1637) ([14], с. 5—66).
Создавая свою философию, Декарт начинает с того, что принимает лишь те факты, которые представляются ему несомненными. Каким же образом удается ему провести различие между приемлемыми и неприемлемыми фактами? В своих «Правилах для руководства ума» (написанных в 1628 г., но опубликованных лишь посмертно) Декарт утверждает: «В предметах нашего исследования надлежит отыскивать не то, что о них думают другие или что мы предполагаем о них сами, но то, что мы ясно и очевидно можем усмотреть или надежно дедуцировать, ибо знание не может быть достигнуто иначе» ([15], с. 55). Человеческий разум непосредственно, силой интуиции, воспринимает основные, ясные и очевидные истины, а вывод следствий составляет сущность философии знания. Таким образом, по Декарту, существуют лишь два акта мышления, позволяющих нам получать новое знание без опасения впасть в ошибку: интуиция и дедукция. Однако в своих «Правилах для руководства ума» Декарт отдает предпочтение интуиции:
Πод интуицией я разумею не веру в шаткое свидетельство чувств и не обманчивое суждение беспорядочного воображения, но понятие ясного и внимательного ума, настолько простое и отчетливое, что оно не оставляет никакого сомнения в том, что мы мыслим, или, что одно и то же, прочное понятие ясного и внимательного ума, порождаемое лишь естественным светом разума и благодаря своей простоте более достоверное, чем сама дедукция, хотя последняя и не может быть плохо построена человеком ([15], с. 57).
В «Рассуждениях о методе» Декарт отстаивал существование разума и достоверного, надежного знания, которым разум обладает. Опираясь на первичную интуицию, Декарт пытается в «Размышлениях о методе» доказать существование бога. Затем с помощью рассуждений, явно образующих порочный круг, Декарт убеждает себя в том, что наша интуиция и метод дедукции должны приводить к верным заключениям, поскольку бог не стал бы вводить нас в заблуждение 5. «Под словом «бог»,— утверждает Декарт в «Метафизических размышлениях» (1641),— я подразумеваю субстанцию бесконечную, вечную, неизменную, независимую, всемогущую, создавшую и породившую меня и все остальные существующие вещи» ([16], с. 363).
Что же касается собственно математических истин, то в «Метафизических размышлениях» Декарт говорит следующее: «Я считал наиболее достоверными те истины, которые ясно воспринимал как относящиеся к фигурам, числам и другим материям, принадлежащим арифметике, геометрии и вообще чистой и абстрактной математике... Только математикам дано достичь несомненности и ясности, ибо они исходят из того, что наиболее легко и просто». Источником математических понятий и истин являются не ощущения. Они носят врожденный характер и присущи нашему разуму от рождения; наделяет же ими наш разум сам бог. Чувственное восприятие материального треугольника не может помочь разуму составить представление об идеальном треугольнике. Для разума вполне очевидно, что сумма углов треугольника должна быть равна 180°.
Затем Декарт обращается к физическому миру. Можно не сомневаться, утверждает он, в том, что интуитивные представления, ясно сознаваемые разумом, и получаемые из них дедуктивные заключения применимы к физическому миру. Декарту было ясно, что бог при сотворении мира руководствовался математическими принципами. В «Рассуждениях о методе» он говорит о существовании «законов, установленных богом в природе, и понятий, запечатленных им в наших душах. Коль скоро мы достаточно поразмыслим над ними, то не станем более сомневаться в их проявлениях во всем, что существует и происходит в мире».
Далее Декарт утверждает, что законы природы неизменны, так как составляют неотъемлемую часть предустановленного богом математического плана. Еще до выхода в свет «Рассуждения о методе» Декарт в письме от 15 апреля 1630 г., адресованном отцу Марену Мерсенну, теологу и близкому другу математиков 6, утверждал:
Не бойтесь всюду провозглашать, что бог установил эти законы в природе так же, как суверен устанавливает законы в своем королевстве... И подобно тому как король обретает тем большее величие, чем меньше знают его подданные, мы считаем величие бога непостижимым и не мыслим себя без небесного царя. Кто-нибудь возразит Вам, заметив, что если 6οι установил эти истины, то он же может изменить их, как изменяет король свои законы. На подобное возражение следует ответить, что такое действительно возможно, если может изменяться божья воля. Я не считаю эти истины вечными и неизменными по тем же причинам, по которым сужу о боге.
В приведенном отрывке из письма Декарт отрицает распространенное в его времена мнение о том, что бог непрестанно вмешивается во все, что происходит в природе7.
Для изучения физического мира Декарт хотел бы использовать только математику, ибо, по его собственному признанию в «Рассуждении о методе», «из всех, кто когда-либо занимался поиском истины в науках, только математикам удалось получить некие доказательства, т. е. указать причины, очевидные и достоверные». По мнению Декарта, одной лишь математики было бы вполне достаточно для изучения физического мира. В «Принципах философии» (1644) он пишет:
Я прямо заявляю, что мне неизвестна иная материя телесных вещей, как только всячески делимая, могущая иметь фигуру и движимая, иначе говоря, только та, которую геометры обозначают названием величины и принимают за объект своих доказательств; я ничего в этой материи не рассматриваю, кроме ее делений, фигур и движения 8, и, наконец, ничего не сочту достоверным относительно нее, что не будет выведено с очевидностью, равняющейся математическому доказательству. И так как этим путем, как обнаружится из последующего, могут быть объяснены все явления природы, то, мне думается, не следует в физике принимать других начал, кроме вышеизложенных, да и нет оснований желать их. ([16], с. 504—505.)
В «Принципах философии» Декарт прямо называет математику сущностью всех наук. По словам Декарта, он «не приемлет и не надеется найти в физике каких-либо принципов, отличных от тех, которые существуют в Геометрии или в Абстрактной Математике, потому, что они позволяют объяснить все явления природы и привести доказательства, не оставляющие сомнений». Объективный мир, по Декарту, есть не что иное, как материализованное пространство или воплощенная геометрия. Его свойства поэтому должны выводиться из первых принципов геометрии (термин «геометрия» Декарт и его современники употребляли практически как синоним математики, так как геометрия тогда составляла значительную часть всей математики ").
Размышлял Декарт и над вопросом, почему мир должен быть доступен анализу математическими средствами. По мнению Декарта, наиболее фундаментальными и надежными свойствами материи являются форма, протяженность и движение в пространстве и во времени. Все эти свойства поддаются математическому описанию. Так как форма сводится к протяженности, Декарт утверждал: «Дайте мне протяженность и движение, и я построю Вселенную». Все физические явления, добавляет Декарт,— результат механического действия молекул, приводимых в движение силами. Силы также подчиняются неизменным математическим законам.
Каким образом объяснял Декарт вкусы, запахи, краски, тембр, высоту и громкость звуков, если внешний мир, по его воззрениям, состоял лишь из движущейся материи? В этих вопросах Декарт принял точку зрения греков, а именно учение Демокрита о первичных и вторичных качествах. Первичные качества — материя и движение — существуют в физическом мире; вторичные качества — вкус, запах, цвет, тепло, приятность или резкость звука — не более чем результат воздействия первичных качеств на органы чувств человека, осуществляемого бомбардировкой этих органов внешними атомами. Реальный мир — совокупность допускающих математическое описание движений предметов в пространстве и во времени, а вся Вселенная в целом представляет собой огромную гармоничную машину, построенную на математической основе. Естественные науки (а в действительности любая дисциплина, пытающаяся установить порядок и меру) подчинены математике. Правило IV декартовских «Правил для руководства ума» гласит:
К области математики относятся только те науки, в которых рассматривается либо порядок, либо мера, и совершенно несущественно, будут ли это числа, фигуры, звезды, звуки или что-нибудь другое, в чем отыскивается эта мера, таким образом, должна существовать некая общая наука, объясняющая все относящееся к порядку и мере, не входя в исследование никаких частных предметов, и эта наука должна называться не иностранным, но старым, уже вошедшим в употребление именем всеобщей математики, ибо она содержит в себе все то, благодаря чему другие науки называются частями математики. Насколько она превосходит своей легкостью и доступностью все эти подчиненные ей науки, видно из того, что она простирается на предметы всех этих наук, так же как и многих других, и если она заключает в себе некоторые трудности, то такие же трудности содержатся и в последних, имеющих сверх того и другие ... . ([15], с. 68.)
Вклад Декарта собственно в математику сводится не к открытию новых истин, а к введению мощного метода, который мы ныне называем аналитической геометрией (гл. V) 10. Появление аналитической геометрии технически революционизировало методологию математики.
Декарт внес заметный вклад и в естествознание, хотя по величине и значимости он несравним с достижениями Коперника, Кеплера или Ньютона. Теория вихрей Декарта (гл. III) была ведущей космологической теорией XVII в. Декарт стал основоположником философии механицизма, согласно которой все явления природы, в том числе все отправления человеческого тела (но не душа), сводятся к движениям частиц, подчиняющимся законам механики. В самой механике Декарт сформулировал закон инерции, ныне известный как первый закон Ньютона: если на тело не действуют никакие силы и оно находится в состоянии покоя, то оно будет и дальше пребывать в состоянии покоя, а если тело движется, то оно будет продолжать прямолинейно двигаться с постоянной скоростью.
Еще одним увлечением Декарта была оптика (расчет линз). Часть «Геометрии» Декарта и вся «Диоптрика», задуманная им как приложение к «Рассуждению о методе», посвящены оптике. Вместе с Виллебродом Снеллиусом Декарт разделяет честь открытия закона преломления света, описывающего, что происходит со светом при резком изменении свойств среды, в которой он распространяется, например при переходе из воздуха в стекло или воду. Начало математизации оптики положили еще греки, но первым, кто систематически изложил оптику как математический предмет, был Декарт. Он внес также важный вклад в географию, метеорологию, ботанику, анатомию (он собственноручно производил вскрытия трупов животных), зоологию, психологию и даже медицину.
Хотя картезианская философия, т. е. философские и естественнонаучные взгляды Декарта и его последователей, в чем-то и противоречила учению Аристотеля и средневековой схоластике, в одном важном отношении Декарт все же был схоластом: все утверждения о природе сущего и реальности он строил на основе чистого разума. Декарт верил в априорные истины и в то, что разум своей силой может выработать полное знание обо всем. Так, Декарт на основе априорных рассуждений сформулировал законы движения. (Работая над биологическими и некоторыми другими проблемами, Декарт в действительности производил эксперименты и делал важные выводы из своих наблюдений. Но даже сводя явления природы к их чисто механическим проявлениям, Декарт многое сделал, чтобы избавить науку от мистицизма и оккультизма.)
Свою лепту в общее убеждение в истинности математики и математического фундамента естествознания внес и великий математик XVII в. (хотя и не столь влиятельный философ, как Декарт) Блез Паскаль (1623—1662). В отличие от Декарта, говорившего о семо-очевидных для разума интуитивных понятиях, Паскаль говорил об истинах, воспринимаемых душой. Истина должна быть либо «самоочевидной» для души, либо логическим следствием подобных истин. В своих «Мыслях» Паскаль сообщает нам следующее:
Наше знание первых принципов, таких, как пространство, время, движение, число, достоверно, как всякое знание, получаемое нами путем умозаключений. В действительности же это знание дает нам душа, и инстинкт есть необходимый фундамент, на котором наш разум строит свои заключения. Требовать от души доказательства первых принципов, прежде чем согласиться принять их, для разума столь же бессмысленно и абсурдно как для души требовать интуитивного представления о всех утверждениях, доказываемых разумом, прежде чем принять их.
Для Паскаля наука — это исследование сотворенного богом мира. Заниматься наукой ради удовольствия дурно. Видеть конечную цель науки в удовольствии означает совращать исследование с истинного пути, ибо при таком подходе тот, кто занимается наукой, обретает «голод или тягу к учению, ненасытную жажду знаний» п. «Такое занятие наукой проистекает из априорного взгляда на себя как на центр всего, а не из стремления искать во всех окружающих явлениях природы присутствие бога и его славу».
Среди выдающихся мыслителей, стоявших у колыбели современной математики и естествознания, Галилео Галилей (1564—1642) занимает столь же почетное место, как и Декарт. Разумеется, Галилей также разделял убеждение, что природа сотворена по математическому плану и что творцом плана был сам господь бог. Широкую известность получил следующий отрывок из небольшого сочинения Галилея «Пробирных дел мастер» (1623):
Философия природы написана в величайшей книге, которая всегда открыта перед нашими глазами,— я разумею Вселенную, но понять ее сможет лишь тот, кто сначала выучит язык и постигнет письмена, которыми она начертана. А написана эта книга на языке математики, и письмена ее — треугольники, окружности и другие геометрические фигуры, без коих нельзя понять по-человечески ее слова: без них — тщетное кружение в темном лабиринте 12.
Итак, природа проста и упорядоченна, и все происходящее в ней закономерно и необходимо. Природа действует в соответствии с совершенными и неизменными математическими законами. Источником всего рационального в природе является божественный разум. Бог вложил в мир строгую математическую необходимость, которую люди постигают лишь с большим трудом, хотя их разум устроен по образу и подобию божественного разума. Следовательно, математическое знание не только представляет собой абсолютную истину, но и священно, как любая строка Священного писания. Исследование природы — занятие столь же благочестивое, как и "изучение Библии. «В действиях Природы господь бог является нам не менее достойным восхищения образом, чем в божественных стихах Писания».
В «Диалоге о двух главнейших системах мира — птолемеевой и коперниковой» (1632) Галилей утверждал, что в математике человек достигает вершины всякого знания, ничуть не уступающего тому знанию, которое является уделом божественного разума. Конечно, божественный разум знает и воспринимает бесконечно больше математических истин, чем человек, но если говорить о достоверности, то те немногие истины, которые доступны человеческому разуму, известны человеку с такой же полнотой, как и богу.
Хотя Галилей был профессором математики и придворным математиком, его главным вкладом в европейскую культуру стали не математические теоремы, а те многочисленные усовершенствования, которые он внес в научный метод. Наиболее значительным из них явился его отказ от поисков физического объяснения, которое Аристотель считал истинной целью естествознания, и переход к поиску математического описания. Различие между этими двумя принципиальными методологическими установками отчетливо видно на следующем примере. Брошенное тело падает на землю, причем падение происходит со все возрастающей скоростью. Аристотель и следовавшие его методологии средневековые ученые пытались найти причину падения тела, предположительно механическую. Вместо поиска причины Галилей описал свободное падение математическим законом, имеющим в современных обозначениях вид s=4,9t2, где s — расстояние (в метрах), которое тело в свободном падении пролетает за t секунд. Эта формула ничего не говорит о том, почему тело падает, и, казалось бы, дает гораздо меньше того, что хотелось бы знать о явлении. Но Галилей был уверен, что знание природы, которого мы стремимся достичь, должно быть описательным. В своей книге «Беседы и математические доказательства, касающиеся двух новых отраслей науки» Галилей устами своего героя Сальвиати утверждал:
Сейчас неподходящее время для занятий вопросом о причинах ускорения в естественном движении, по поводу которого различными философами было высказано столько различных мнений: одни приписывали его приближению к центру, другие — постепенному частичному уменьшению сопротивления среды, третьи — некоторому воздействию окружающей среды, которая смыкается позади падающего тела и оказывает на него давление, как бы постоянно его подталкивая; все эти предположения и еще многие другие следовало бы рассмотреть, что, однако, принесло бы мало пользы. Сейчас для нашего автора будет достаточно, если мы рассмотрим, как он исследует и излагает свойства ускоренного движения (какова бы ни была причина ускорения), приняв, что моменты скорости, начиная с перехода от состояния покоя, идут возрастая в том же простейшем отношении, как и время ([17], с. 243—244.). Итак, по Галилею, содержательные научные вопросы следовало отделить от поиска «причины причин» и отказаться от чисто умозрительных рассуждений о физических предпосылках явлений. Галилей мог бы сформулировать свою идею в виде следующей максимы для ученых: ваше дело не рассуждать — почему, а устанавливать — сколько (т. е. находить количественные соотношения).
Весьма вероятно, что первая реакция на этот пункт намеченной Галилеем программы даже в наши дни была бы отрицательной. Описание явлений на языке формул не более чем первый шаг исследования, возразили критики. Истинная функция науки в действительности была осознана последователями Аристотеля и состоит в объяснении причин, по которым происходит явление. Даже Декарт возражал против установки Галилея на поиск описательных формул, «Все, что Галилей говорит о телах, свободно падающих в пространстве,— утверждал Декарт,— лишено всякого основания, так как сначала ему надлежало бы установить природу тяжести». Кроме того, продолжал Декарт, Галилею следовало бы поразмыслить о первопричинах наблюдаемого явления. Но, как мы теперь знаем, принятое Галилеем решение ограничиться описанием явления было наиболее глубоким и наиболее плодотворным новшеством, когда-либо внесенным в методологию естествознания. Как станет ясно из дальнейшего, значение этого нововведения состояло в том, что оно более четко и определенно, чем ранее, поставило естествознание под эгиду математики.
Еще один методологический принцип, выдвинутый Галилеем, состоял в том, что любая область естествознания должна быть построена по образу и подобию математики. Здесь необходимо выделить два существенных момента. Математика начинает с аксиом, т. е. самоочевидных, ясных истин. Из них с помощью дедуктивного вывода она устанавливает новые истины. Следовательно, любая область естественных наук также должна начинать с аксиом, или принципов, и строиться дедуктивно. Кроме того, из исходных аксиом надлежит извлекать как можно больше следствий. Такой же план, по существу, был предложен еще Аристотелем, видевшим конечную цель в дедуктивной структуре естественных наук, образцом для которых должна служить математика.
Но в том, что касается способа получения первых принципов, Галилей решительно отошел от греков, мыслителей средневековья и Декарта. Предшественники Галилея и Декарт усматривали источник первых принципов в человеческом разуме. Стоит лишь разуму поразмыслить над любым кругом явлений, как он тотчас же постигнет фундаментальные истины. При этом в качестве примера, подтверждающего всесилие человеческого разума, обычно ссылались на математику. Такие аксиомы, как «Если к равным [частям] прибавить равные, то получатся равные же [части]» или «Через любые две точки можно провести прямую, и притом только одну», якобы самопроизвольно возникают, когда мы начинаем размышлять о числах или о фигурах,— и они считались неоспоримыми истинами. Греки установили несколько физических принципов, которые в их глазах были столь же привлекательными, как математические аксиомы. Так, они считали вполне очевидным, что все тела во Вселенной должны занимать определенное (естественное) место. Не менее очевидным казалось и то, что состояние покоя более согласуется с сутью вещей, чем состояние движения. Не подлежало сомнению и утверждение о том, что, для того чтобы привести тело в состояние движения и далее поддерживать это состояние, к нему необходимо приложить определенную силу. Вера в то, что человеческий разум способен сам по себе выработать фундаментальные принципы, не отрицает пользу наблюдений для установления первых принципов. Но наблюдения как бы помогают разуму припомнить первые принципы, подобно тому как при взгляде на знакомое лицо в памяти всплывают различные сведения о нем.
Все эти ученые, по мнению Галилея, сначала решали, как должен был бы функционировать мир в соответствии с предустановленными первыми принципами. Галилей же считал, что в физике в отличие от математики источником первых принципов должны быть эксперимент и анализ его результатов. Чтобы получать правильные и фундаментальные первые принципы, физику надлежит с большим вниманием прислушиваться к голосу природы, а не к тому, чему отдает предпочтение разум. Галилей открыто критиковал естествоиспытателей и философов, принимавших те или иные «законы» только потому, что те согласовывались с их априорными представлениями относительно того, как должна была бы вести себя природа. Природа, утверждал Галилей, не сотворила сначала мозг человека, а затем мир так, чтобы он был воспринимаем человеческим разумом. В адрес средневековых схоластов, вторивших Аристотелю и занимавшихся толкованием различных суждений в его сочинениях, Галилей язвительно заметил, что знание берется из наблюдений, а не из книг. Бесполезно спорить об Аристотеле. Те, кого он называл бумажными учеными, хотели бы уподобить естественнонаучные исследования изучению «Энеиды» или «Одиссеи» и превратить науку о природе в свод текстов. «Перед законом природы бессильны любые авторитеты».
Некоторые ученые эпохи Возрождения и современник Галилея Фрэнсис Бэкон (1561—1626) также пришли к выводу о необходимости экспериментального подхода к изучению природы. В этом пункте своей программы Галилей не намного опередил других 18 . Тем не менее Декарт не смог по достоинству оценить мудрость галилеевского подхода с его упором на эксперимент. Наши органы чувств, утверждал Декарт, способны лишь вводить в заблуждение. Только разум может развеять туман подобных заблуждений и постичь истину. Из врожденных первых принципов, постигаемых разумом, мы можем выводить явления природы и понимать их. В действительности, как мы уже упоминали, Декарт в своей научной работе широко использовал эксперимент и требовал, чтобы теория находилась в согласии с экспериментом, однако в своей философии он продолжал связывать истины4 исключительно разумом.
Мнение Галилея о том, что один лишь разум не может служить источником правильных физических представлений, разделяли лишь немногие физики. Так, взгляды Декарта критиковал Христиан Гюйгенс. С критикой чистого рационализма выступали и английские физики. Обращаясь к членам Королевского общества, Роберт Гук (1635—1705) заявил: «Имея перед глазами так много фатальных примеров ошибок и заблуждений, совершенных большей частью человечества, когда она опиралась только на силу человеческого разума, мы начали теперь проверять все гипотезы свидетельством органов чувств».
Разумеется, Галилей понимал, что эксперимент может привести к неправильному принципу и что дедуктивный вывод из неверного принципа порождал бы ошибочные заключения. Он предлагал и, по-видимому, использовал эксперименты для проверки своих умозаключений и для отбора первых принципов. Но вопрос о том, сколь широко экспериментировал сам Галилей, остается открытым. Некоторые из предложенных им экспериментов иногда называют «мысленными»: Галилей лишь мысленно представлял, что должно получиться в результате такого эксперимента. Тем не менее выдвинутый им принцип, согласно которому физические принципы должны опираться на эксперимент и наблюдение, был революционным и имел решающее значение. Сам Галилей не сомневался в том, что некоторые из принципов, использованных богом при сотворении мира, могут быть постигнуты чистым разумом, но, проложив путь эксперименту, Галилей одновременно заронил и сомнения. Если источником основных принципов естествознания должен быть эксперимент, то не должен ли эксперимент служить источником и математических аксиом? Этот вопрос не беспокоил ни самого Галилея, ни его преемников вплоть до начала XIX в. Математика продолжала наслаждаться своим привилегированным положением.
Свою естественнонаучную деятельность Галилей сосредоточил на проблемах материи и движения. Он независимо от Декарта установил принцип инерции, ныне известный как первый закон движения Ньютона. Галилею удалось также получить законы движения поднимающихся вертикально вверх и падающих тел, движения тел по наклонной плоскости, а также тел, брошенных под некоторым углом к горизонту. Галилей показал, что тело, брошенное под углом к горизонту, движется по параболе. Резюмируя, можно сказать, что Галилей исследовал законы движения земных тел. И хотя, как во всяком большом открытии, у Галилея заведомо были предшественники, никто из них не сознавал с такой ясностью идеи и принципы, которым должно руководствоваться научное исследование, и не проводил эти принципы в жизнь столь просто и эффективно.
Будучи глубоко новаторской по духу, философия и методология науки Галилея подготовила почву для свершений Исаака Ньютона, который родился в тот самый год, когда ушел из жизни Галилей.
.27.12.2022, ../data/doc/art/2017/6.htm



 ЗАКРЫТЬ
ЗАКРЫТЬ